PostgreSQL Indexes: B-Tree
Table of Contents
Indexes in relational databases are a very imporatant feature, that reduce the cost of our lookup queries. In the last post on the basics of indexes in PostgreSQL, we covered the fundamentals and saw how we can create an index on a table and measure it’s impact on our queries. In this post, we will take a dive into the inner workings and some implmentation details of the most used index type in PostgreSQL - the B-Tree index.
What is B-Tree? #
From Wikipedia’s page on B-Tree:
In computer science, a B-tree is a self-balancing tree data structure that keeps data sorted and allows searches, sequential access, insertions, and deletions in logarithmic time.
Awesome, right? Basically, it’s a data structure that sorts itself. That’s why it’s self-balancing - it chooses it’s shape on it’s own.
The B-tree is a generalization of a binary search tree in that a node can have more than two children. Unlike self-balancing binary search trees, the B- tree is optimized for systems that read and write large blocks of data.
Unlike regular binary trees, the B-Tree can have multiple leaves, which it balances on it’s own. Also, it’s implementations are I/O optimized, which makes them suitable for database indexes.
B-trees are a good example of a data structure for external memory. It is commonly used in databases and filesystems.
Now, there’s plenty to know about B-Trees. Knowing how they work is pretty interesting, so let’s check it out.
Functionality #
As a disclaimer before we start with the B-Tree as a self-balancing data structure, I would like to inform you that there is a lot of CS theory about the B-Tree, which we will not cover in this section. For example, you might want to look first at binary trees, 23-trees and 234-trees before you dive into B-Trees. Nevertheless, what we will cover here will be sufficient for you to understand how the B-Tree index works.
Having that out of the way, think of a binary tree. In binary trees, each node can have a maximum of two children, hence the name - binary.
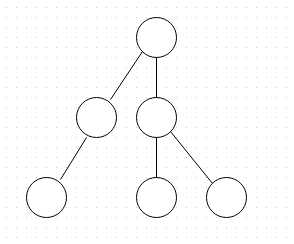
A Binary Tree
Well, a B-Tree is a tree where each node can have multiple children, or better said, a B-Tree can have N children. While in binary search trees each node can have one value, B-Trees have the concept of keys. Keys are like a list of values, that each of the nodes will hold.
B-Trees also have the concept of order, where for B-Trees an order of 3 means that each non-leaf node of the tree can have a maximum of 3 children. Having that in mind, this means that each node can have two (3-1) keys.
Confusing? Well, think about this: on a non-leaf node with keys 5, 10, you can
add three nodes:
- one node, with values smaller than 5
- one node, with values between 5 and 10
- and one node, with values larger than 10
Let’s draw it out:
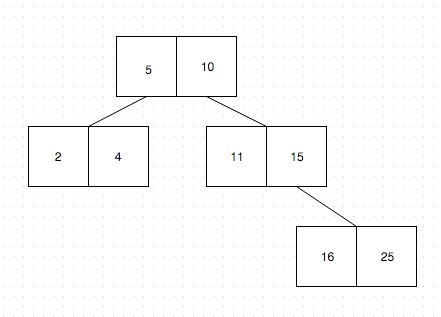
The most important thing about B-Trees is their balaning aspect. The concept revolves on the fact that each node has keys, like in the example above. The way B-Trees balance themselves is really interesting, and the keys are the most important aspect of this this functionality.
Basically, whenever a new item (or, in our case, a number) is added, the B-Tree finds the appropriate place (or, node) for the item to go in. For example, if we want to add the number 6, the B-Tree will “ask the root node”, in what node should it push the number in. “Asking” is nothing more than comparing the new number with the keys of the node. Since the number 6 is larger then 5, but smaller then the number 10 (which are the root node keys), it will create a new node just below the root node:
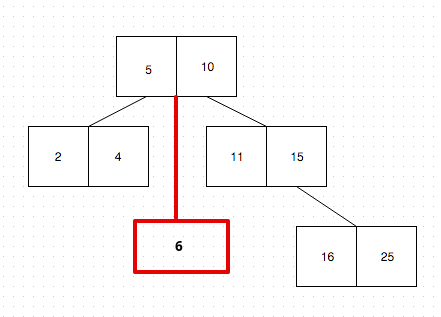
With this mechanism, the B-Tree is always ordered and looking up a value in it is rather cheap. There are multiple implementations of B-Trees. For this post, it’s nice to know that PostgreSQL uses the B-Tree implementation of the “Lehman and Yao’s high-concurrency B-tree management algorithm”. You can read the actual paper here{:target="_blank"}.
But, how is this relevant to the B-Tree indexes in PostgreSQL?
B-Trees and PostgreSQL #
Indexes in PostgreSQL, simply put, are a replica of the data on the column(s) that is/are indexed. The only difference is in the data order - the replica of the data is sorted, which allows PostgreSQL to quickly find and retrieve the data. For example, when you search for a record in a table, where the column by which you are searching is indexed, the index decreases the cost of the query because PostgreSQL looks up in the index and can easily find the location of the data on disk.
The B-Tree data structure falls really nice into place, when you recall that the index is ordered. Under the hood, indexes are B-Trees, but really big ones. Due to the nature of the B-Tree data structure, whenever a new record is added on the indexed table it knows how to rebalance and keep the order of the records in it.
Limitations #
Almost in all use cases, the power of indexes is noticable on large amounts of data. This means that the indexes will have to be as big as the actual data tables. Or does it?
Imagine if we are dealing with billions of records. This means that the index
tables will have the billions of records stored in an ordered fashion. Okay,
PostgreSQL could handle that. But, can you imagine how long would an INSERT
command take? Adding the record in the data table will take really long,
because the index will have to add the new record in the correct place, to keep
the order of the indexes. Due to this limitation, the implementation of the
B-Tree index keeps page files, which simply put, are nodes on a big B-Tree
data structure.
Although each index is a whole, this paging mechanism adds a separation of the data in the index, while still keeping the order. In that case, instead of dumping the whole index into memory just to add a single record, PostgreSQL finds the page where the new record should be added and writes the indexed value into it.
My explanation is quite abstract, but the aim of this article was to introduce the B-Tree data structure and how it falls into place with PostgreSQL. If you would like to read more details on the implementation, check Discovering the Computer Science Behind Postgres Indexes from Pat Shaughnessy. Actually, if I knew of the existence of his article before I started writing this article, I might have not even written it.
Using a B-Tree index #
Having the workings of B-Tree index aside, let’s see how to use it. The command to add an index to a column is:
CREATE INDEX name ON table USING btree (column);Or, since the btree index is the default one, we can omit the USING part of
the command:
CREATE INDEX name ON table;This will create a BTree index on the name column in the table table.
Outro #
In this article we took an overview on one of the most popular indexes in PostgreSQL. We saw what is the difference between Binary Search Trees and B-Trees, and how their behaviour translates into PostgreSQL. Take note, there is a ton of detail that I had to omit due to the length of the article and the target audience.
Links #
If you would like to dig in deeper into B-Tree, whether the index or the data structure, here are some useful links: